Kaggleデータをあさってみる2(Human Resource Analysis)

前回は、Kaggleデータをあさってみる1(Human Resource Analysis)で、人事データを俯瞰してみました。http://ritsuan.com/blog/5840/

Kaggleデータをあさってみる1(Human Resource Analysis)

今回は前回に引き続き、Human Resource Analysisを行っていきます。データは当然前回と同じ、Human Resource Analysisのデータを使用します。
https://www.kaggle.com/ludobenistant/hr-analytics

今回も前回同様に全体を俯瞰することを目的に解析を進めていこうと思います。
前回は、ランダムフォレストによって、目的変数に影響を及ぼしている変数を特定し、２変数での集計・可視化を行いました。

今回は、モデルとしてロジスティック回帰を行い、交互作用項を導入することで、どの変数とどの変数の組み合わせが相乗効果をもたらすか(例えば、ある二つの量的変数が二つとも大きい値であれば、会社を退職しやすいなど)を検出したいと思います!

前回同様に進めていきます。前回と同じところは説明を省略します。
いちいち説明していると量が膨大になりそうなところはさらっと簡潔に説明していますがご了承ください。
そんなにモデル比較するわけでもないので、Accuracy,ROC曲線,AUCのところは、正直今回はいらないのですが、そういっていると結局一度も書かない気がしたのであえて書きました。今後データサイエンスの資格試験ができたら絶対に聞かれるところなので一応わかっていた方がよいです。

それでは参りましょう！

#データの読み込み
t=read.csv(“HR_comma_sep.csv”,header=T)
#データの構造確認
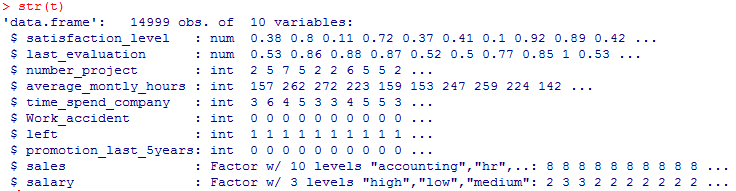
str(t)

#質的変数のFactor化
i=0
d=t
for (i in c(3,5,6,7,8)){
d[,c(i)]=as.factor(t[,c(i)])
}
#結果の確認
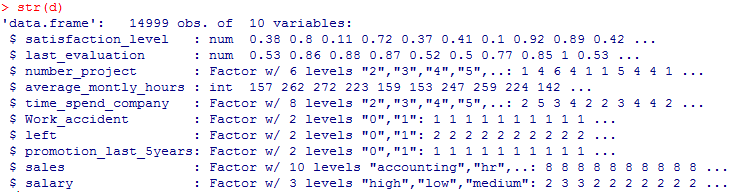
str(d)

#行数の算出
n=nrow(d)
n
#sample関数用の乱数の種をまく
set.seed(123)
#整数1～nから75%の整数を取り出す。
ind=sample(n,floor(n*0.75))
head(ind)

#学習用(train)とテスト用(test)にデータを分割する。
train=d[ind,]
test =d[-ind,]
#結果を見る
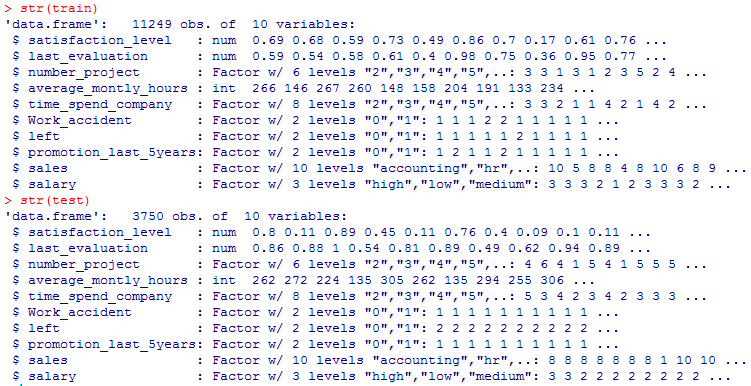
str(train)
str(test)

#SMOTE関数による不均衡データへの対応(今回は、退職した(1)方が一桁少ないので)
install.packages(“DMwR”,dependencies=T)
library(DMwR)
#乱数の種をまく
set.seed(123)
#SMOTE関数でのSMOTEアルゴリズムの実行
train1 = SMOTE(left~., data = train)
#結果確認
str(train1)
table(train1[,7])

#まず通常のロジスティック回帰を行う
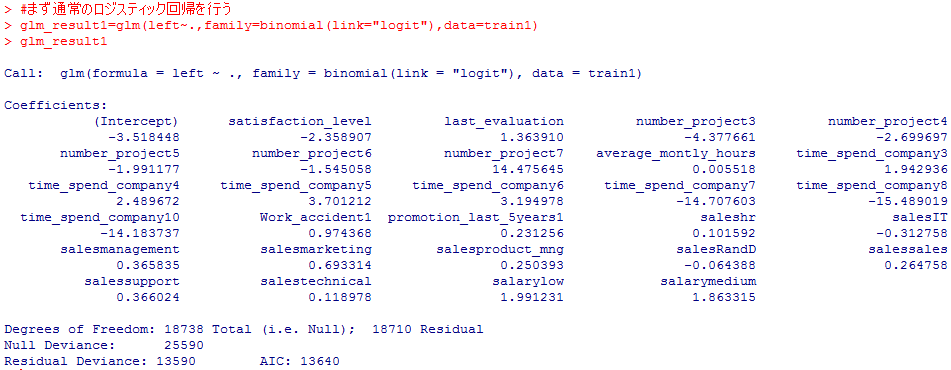
glm_result1=glm(left~.,family=binomial(link=”logit”),data=train1)
glm_result1

#次に交互作用項を導入したロジスティック回帰を行う
glm_result2=glm(left~(.)^2,family=binomial(link=”logit”),data=train1)
glm_result2
本来ロジスティック回帰では、目的変数は0より大きく1より小さい数になるはずですが、(おそらく)小数点以下の桁の扱いのために、0,1の結果も出てしまったようで警告がでましたが、ここでは気にしないで進めます。

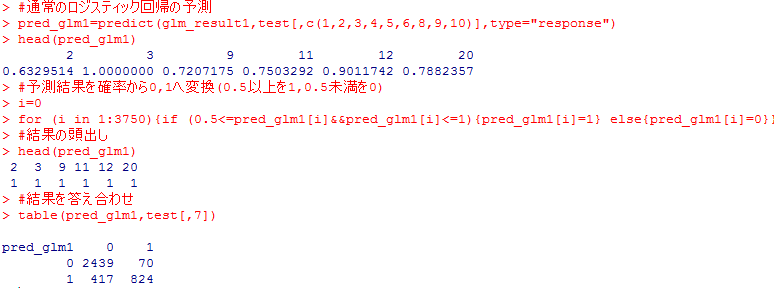
#通常のロジスティック回帰の予測
pred_glm1=predict(glm_result1,test[,c(1,2,3,4,5,6,8,9,10)],type=”response”)
head(pred_glm1)
#予測結果を確率から0,1へ変換(0.5以上を1,0.5未満を0)
i=0
for (i in 1:3750){if (0.5<=pred_glm1[i]&&pred_glm1[i]<=1){pred_glm1[i]=1} else{pred_glm1[i]=0}}
#結果の頭出し
head(pred_glm1)
#結果を答え合わせ
table(pred_glm1,test[,7])

#交互作用項を導入したロジスティック回帰の予測
pred_glm2=predict(glm_result2,test[,c(1,2,3,4,5,6,8,9,10)],type=”response”)
head(pred_glm2)
#予測結果を確率から0,1へ変換(0.5以上を1,0.5未満を0)
i=0
for (i in 1:3750){if (0.5<=pred_glm2[i]&&pred_glm2[i]<=1){pred_glm2[i]=1} else{pred_glm2[i]=0}}
#結果の頭出し
head(pred_glm2)
#結果を答え合わせ
table(pred_glm2,test[,7])
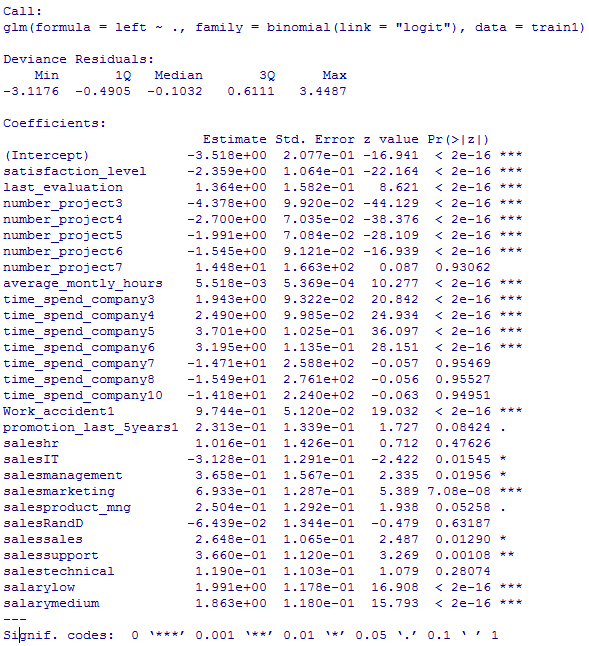
警告が出ていて、おそらく、交互作用項を作るときに、質的変数に対して数量化理論Ⅱの適用して、rankの問題から次元数をひとつ落としていた(例えばある変数内にA、B、CとあったらA,Bしか交互作用項の作成に使用されていないということ)まま、交互作用項を作っており、本当はもっと交互作用項を作れたのに次元数をひとつ落とした時の(質的変数の)一水準が使われていないということなのでしょう。summary(glm_result2)の結果からわかります(後で出てきます)。
正しくないかもと言っていますが、交互作用を作る前と後では、table関数による集計の結果から交互作用項なしでは正しい認識が2439+824個に対して、交互作用をいれた後は、2555+841と精度は向上しているので、問題ないでしょう。

#通常のロジスティック回帰のAccuracy算出(今回は別に必要ないんですが参考までに)
#Accuracy
misclassify_rate1 = mean(pred_glm1 != test[,7])
Accuracy1=1-misclassify_rate1
Accuracy1

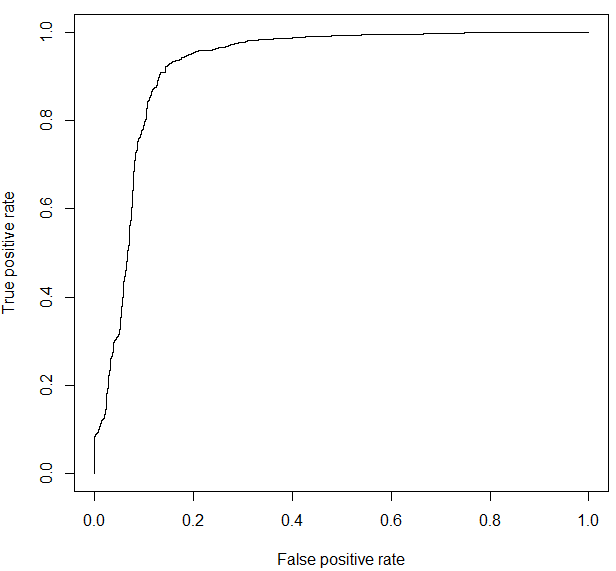
#ROC曲線(ROCRパッケージが入っていなければinstall.packages関数実行してください)
library(ROCR)
p1 = predict(glm_result1, newdata=test[,c(1,2,3,4,5,6,8,9,10)], type=”response”)
pr1 = prediction(p1, test[,7])
prf1 = performance(pr1, measure = “tpr”, x.measure = “fpr”)
plot(prf1)

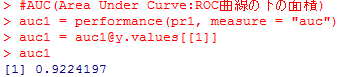
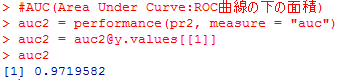
#AUC(Area Under Curve:ROC曲線の下の面積)
auc1 = performance(pr1, measure = “auc”)
auc1 = auc1@y.values[[1]]
auc1

#交互作用項を導入したロジスティック回帰のAccuracy(同様に必要ないです。参考まで。)
#Accuracy
misclassify_rate2 = mean(pred_glm2 != test[,7])
Accuracy2=1-misclassify_rate2
Accuracy2

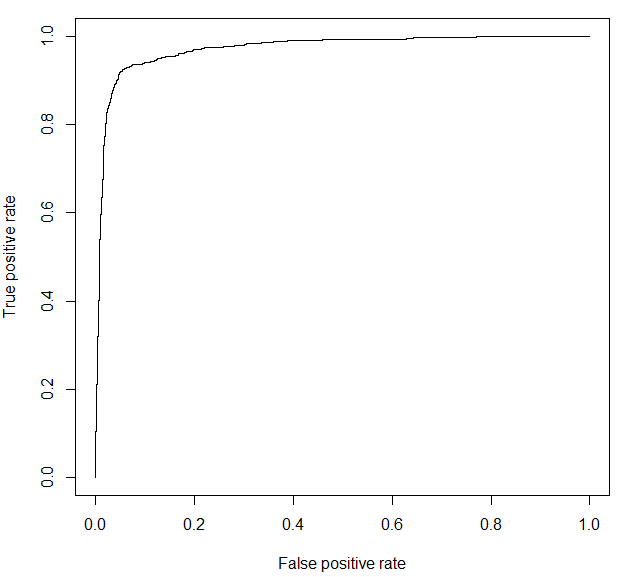
#ROC曲線
p2 = predict(glm_result2, newdata=test[,c(1,2,3,4,5,6,8,9,10)], type=”response”)
pr2 = prediction(p2, test[,7])
prf2 = performance(pr2, measure = “tpr”, x.measure = “fpr”)
plot(prf2)

#AUC(Area Under Curve:ROC曲線の下の面積)
auc2 = performance(pr2, measure = “auc”)
auc2 = auc2@y.values[[1]]
auc2

#通常のロジスティック回帰の説明変数の重要度
summary(glm_result1)

#交互作用項を含めた説明変数の重要度(これが今回の目玉(一応))
summary(glm_result2)

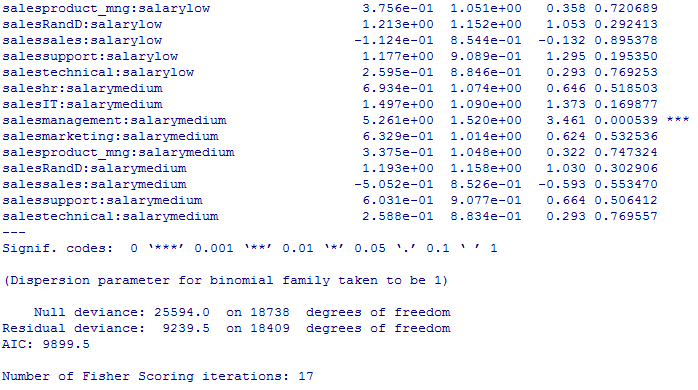当初の目標は、有効な交互作用項を特定することで、特定の二つの変数の特定の値が組み合わさると、仕事をやめることに対してより強い影響を及ぼす、ということを仮定して、その候補を探りました。
その結果得られた、「仕事をやめることに強い作用を及ぼす」二つの変数の組を下にリストアップします。(各変数の右の確率の横についている星印が三つ以上のものを抽出します)

今回は深い内容の検討には踏み込みませんが、次回以降踏み込んでいきます(主にデータの可視化を行います)。
satisfaction_level:last_evaluation
satisfaction_level:number_project3
satisfaction_level:number_project5
satisfaction_level:time_spend_company5
satisfaction_level:time_spend_company6
last_evaluation:number_project3
last_evaluation:number_project6
last_evaluation:average_montly_hours
last_evaluation:time_spend_company3
number_project3:average_montly_hours
number_project3:time_spend_company3
number_project4:time_spend_company3
number_project6:time_spend_company3
number_project4:time_spend_company5
number_project6:time_spend_company5
number_project6:time_spend_company6
average_montly_hours:time_spend_company5
time_spend_company6:salarylow
Work_accident1:promotion_last_5years1
salesmanagement:salarylow
salesmanagement:salarymedium

今後の解析手順ですが、
・片方が質的変数の一水準なものは、その水準でデータを抽出してきて、left(0,1)で二群にわけて、もう片方の量的変数で箱ひげ図を描けばよいでしょう。
・両方が質的変数の一水準なものは、その水準でデータを抽出してきてその中にleft(0),left(1)が何対何で含まれているか見ればよいでしょう。
・両方が量的変数なものは、散布図にplotして、left(0,1)で点の色を黒と赤に無理分ければよいでしょう。

今回は、とりあえず、交互作用項の抽出までやりました。
それでは今回はここまで。

鈴木瑞人
東京大学大学院 新領域創成科学研究科　メディカル情報生命専攻　博士課程1年
東京大学機械学習勉強会　代表
NPO法人Bizjapan technology部門BizXチームリーダー