2022.06.02 Thu | お知らせ

奄美教育フェス2022「違いを豊かさに」を、瀬戸内町きゅら島交流館にて、6月5日に開催いたします。 掛川で2回開催した教育フェスを、鹿児島の奄美に広げて企画することとなりました。 教育格差が問題視される中、リツアンだから […]
続きを読む >>
2022.06.02 Thu | お知らせ

奄美教育フェス2022「違いを豊かさに」を、瀬戸内町きゅら島交流館にて、6月5日に開催いたします。 掛川で2回開催した教育フェスを、鹿児島の奄美に広げて企画することとなりました。 教育格差が問題視される中、リツアンだから […]
続きを読む >>2022.01.31 Mon | スタッフの日常

世界的に活躍されている指揮者・芸術監督の木許裕介さんが、弦楽旅団「キャラバン・ストリングス」を率い、11月23日にコンサートを開催しました。 23日の掛川市生涯学習センター大ホールでのコンサート本番だけなく、掛川の街の至 […]
続きを読む >>2022.01.31 Mon | スタッフの日常

当社のパートナーでもあり、世界的に活躍されている指揮者・芸術監督の木許裕介さんが、弦楽旅団「キャラバン・ストリングス」を率い、11月23日にコンサートを開催しました。 しかし、今回の見どころは、23日の掛川市生涯学習セン […]
続きを読む >>2023.01.23 Mon | スタッフの日常

リツアンSTCが支援させていただいている、アフリカのモザンビークで活動するNPOアシャンテママ。(リツアンCSRページはこちら) 創設者の栗山さやかさんが、なぜ遠く離れた地の親子を支える活動を始めたのか。その半生をまとめ […]
続きを読む >>2020.09.23 Wed | お知らせ

自粛の日々が続く今、少しずつ日常は戻りつつも、コロナの影響を強く受けている方も多いと思います。 直接お会いできない中でも、みなさんの何かの力になりたいと考え、「給付金申請サポート」を行うことにしました。 「給付金があるら […]
続きを読む >>2020.06.05 Fri | スタッフの日常
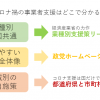
新型コロナへの対応で、あらゆる会社がそれぞれに対応に苦しんでいます。 それを助ける公的な「事業者支援」が立ち上がっていますが、そもそも知らなかったり、申請の仕方も不安な事業者さんが多いのではないでしょうか。 […]
続きを読む >>2020.05.18 Mon | スタッフの日常
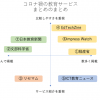
コロナの影響を強く受けている教育領域。 今、家庭学習を支えるために、多くの企業や自治体が、様々なツール、オンラインコンテンツを無償で公開しています。 しかし、たくさんの支援が集まったために、「多すぎて選べない」という悩み […]
続きを読む >>2020.05.01 Fri | スタッフの日常

東大卒でファシリテーター/編集者をしている杉山大樹です。 リツアンに4月から所属しています。ブログは引き続き担当です! 外に出れないGWなんて、おしまいだ..。 子供も辛いけど、辛そうな子供を見る親も辛い。 ゲームやYo […]
続きを読む >>2020.04.12 Sun | スタッフの日常

東大卒でファシリテーター/編集者をしている杉山大樹です。 (4月から正式にリツアンに入社することになりました。よろしくお願いします!) リツアンは実は本州に留まらず、沖縄にもつながりがあります。 特に仲良しなのが、沖縄の […]
続きを読む >>2020.01.21 Tue | スタッフの日常

実はこの間に、東大新卒フリーランスから会社に勤め始めた杉山です!(フリーの仕事も続けてます!) お世話になっているリツアンのみなさんに転職のご挨拶に行ったところ、 社長クニさんから 「いつやめんの?待ってるね!」 という […]
続きを読む >>