Kaggleデータをあさってみる3(Human Resource Analysis)

前回は、Human Resource Analysisのデータで、交互作用項入りのロジスティック回帰を行い、説明変数同士の交互作用を検討し、交互作用のある説明変数同士の組の候補を挙げました。
http://ritsuan.com/blog/5879/

今回はその候補を一つずつ検討していきたいと思います。
前回候補に挙がった変数の組は以下になります。
satisfaction_level:last_evaluation
satisfaction_level:number_project3
satisfaction_level:number_project5
satisfaction_level:time_spend_company5
satisfaction_level:time_spend_company6
last_evaluation:number_project3
last_evaluation:number_project6
last_evaluation:average_montly_hours
last_evaluation:time_spend_company3
number_project3:average_montly_hours
number_project3:time_spend_company3
number_project4:time_spend_company3
number_project6:time_spend_company3
number_project4:time_spend_company5
number_project6:time_spend_company5
number_project6:time_spend_company6
average_montly_hours:time_spend_company5
time_spend_company6:salarylow
Work_accident1:promotion_last_5years1
salesmanagement:salarylow
salesmanagement:salarymedium

前回書いたように、解析手順は、
今後の解析手順ですが、
(1)片方が量的変数で片方が質的変数の一水準なものは、その水準でデータを抽出してきて、left(0)left(1)で二群にわけて、もう片方の量的変数で箱ひげ図を描く。
(2)両方が質的変数の一水準なものは、その水準でデータを抽出してきてその中にleft(0),left(1)が何対何で含まれているか見る。
(3)両方が量的変数なものは、散布図にplotして、left(0,1)で点の色を黒と赤に無理分ける。
というようになります。
なので上の変数の組をこの３つに分類してみましょう。

(1)片方が量的変数で片方が質的変数の一水準なもの
(1-1)satisfaction_level:number_project3
(1-2)satisfaction_level:number_project5
(1-3)satisfaction_level:time_spend_company5
(1-4)satisfaction_level:time_spend_company6
(1-5)last_evaluation:number_project3
(1-6)last_evaluation:number_project6
(1-7)last_evaluation:time_spend_company3
(1-8)number_project3:average_montly_hours
(1-9)average_montly_hours:time_spend_company5
(2)両方が質的変数の一水準なもの
(2-1)number_project3:time_spend_company3
(2-2)number_project4:time_spend_company3
(2-3)number_project6:time_spend_company3
(2-4)number_project4:time_spend_company5
(2-5)number_project6:time_spend_company5
(2-6)number_project6:time_spend_company6
(2-7)time_spend_company6:salarylow
(2-8)Work_accident1:promotion_last_5years1
(2-9)salesmanagement:salarylow
(2-10)salesmanagement:salarymedium
(3)両方が量的変数なもの
(3-1)satisfaction_level:last_evaluation
(3-2)last_evaluation:average_montly_hours

という風に分類されます。各組み合わせに対して、(1-1)～(3-2)というタグをつけておきました。
それでは、交互作用項の候補の詳細な検討に入りたいと思います。

この解析で期待している結果としては、例えば、
「あるタスク数でかつ月の労働時間が特定の時間になると社員は著しく辞めやすくなる」、などという相乗効果や、「月の労働時間が長くても、特定の条件が重なると、著しく辞めにくくなる」、などという相乗効果です。

ます、前回同様、データの読み込みからやっていきます。
#データの読み込み
t=read.csv(“HR_comma_sep.csv”,header=T)
#データの構造確認
str(t)

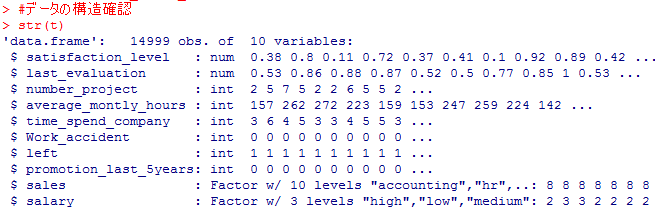
#質的変数のFactor化
i=0
d=t
for (i in c(3,5,6,7,8)){
d[,c(i)]=as.factor(t[,c(i)])
}
#結果の確認
str(d)

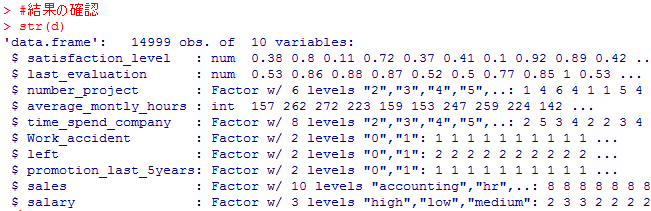
それでは、交互作用項を検討してきましょう。
(1-1)satisfaction_level:number_project3
(1-2)satisfaction_level:number_project5
に関して、
可視化はhadley wickhamさんが作成したggplot2を使います。
#ggplot2パッケージのダウンロード・インストール
install.packages(“ggplot2”,dependencies=T)
library(ggplot2)

#データの可視化
ggplot(data = d, mapping = aes(x = left, y = satisfaction_level)) +
geom_boxplot()+
facet_wrap(~ number_project, nrow = 1)
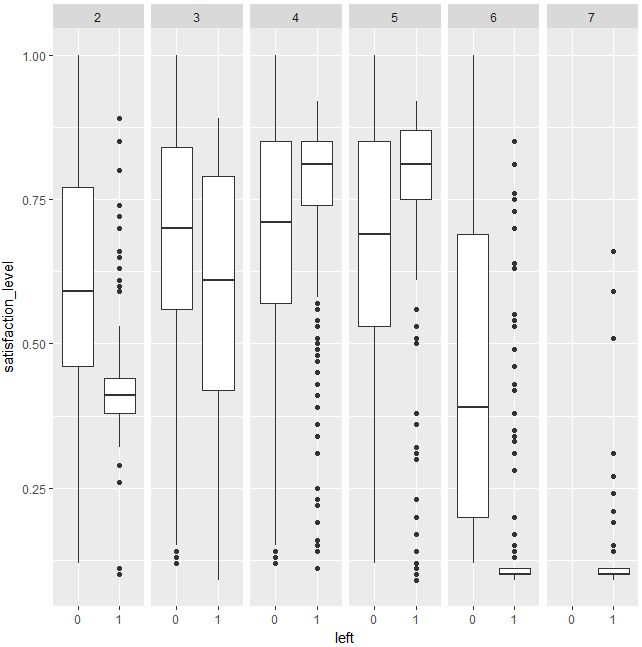たしかに、number_projectが3または5であり、かつsatisfaction_levelが高ければ、辞める人が多くなることがわかります。しかし、なぜ、number_projectが4のときが検出できていないのでしょうか？
実際にヒストグラムを作成して見ていこうと思います。
ggplot(data=d, aes(x=satisfaction_level, fill=left))+
geom_bar()+
facet_wrap(~ number_project, nrow = 1)

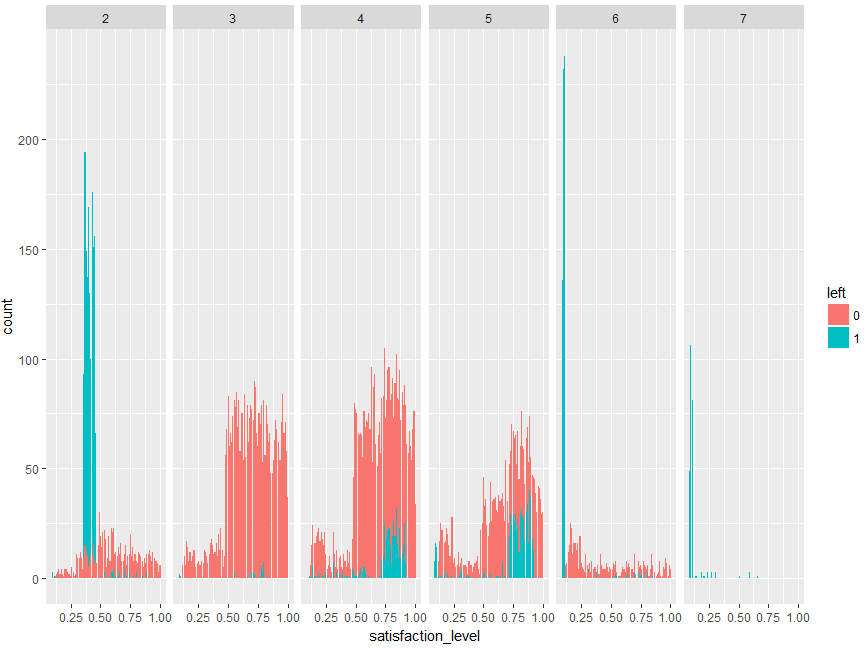
number_projectが4のときは確かに満足度が高いほど、仕事をやめる人も増えるのですが、辞めない人も増えるので、重要な交互作用項としては検出されなかったみたいですね。
それでは、number_project=3,5に関して順に詳細を見ていきましょう。

(1-1)number_project=3に関しては、left=1(辞めた人)が極端に少なく、satisfactation_levelが高いことと、number_project=3という条件が”辞めない”ことに関して相乗効果があることがわかります(これを相乗効果ということに関して異論がある方もいるかと思いますが、今回はシンプルに説明したく相乗効果と呼びます)。

(1-2)number_project=5に関しては、left=1(辞めた人)がsatisfactation_levelが高いところに多く、satisfactation_levelが高いことと、number_project=5という条件は、”辞める”ことに関して相乗効果があるといえそうです。

以上としては会社としては、社員に対して、それぞれプロジェクトを3つもたせ、仕事への満足度が高い状態にしておけば、会社にとどまってくれることがわかります。
逆に、社員にプロジェクトを5個もたせると、仕事への満足度は高いけれども、辞めてしまうことがわかります。仕事への満足度調査に表れていないことがミソです。
プロジェクト数が6個以上で、満足度が低い社員は、ほぼ確実に会社をやめるため、まずプロジェクト数を６個以上もたせないことと、もしやむ終えず持たせた場合には、常に仕事への満足度を調査し、満足度が下がっていたらすぐにプロジェクト数を減らしてあげる必要があります。

さて次は、
(1-3)satisfaction_level:time_spend_company5
(1-4)satisfaction_level:time_spend_company6
の詳細を見ていきたいと思います。
まずは、箱ひげ図から見てみましょう。
ggplot(data = d, mapping = aes(x = left, y = satisfaction_level)) +
geom_boxplot()+
facet_wrap(~ time_spend_company, nrow = 1)
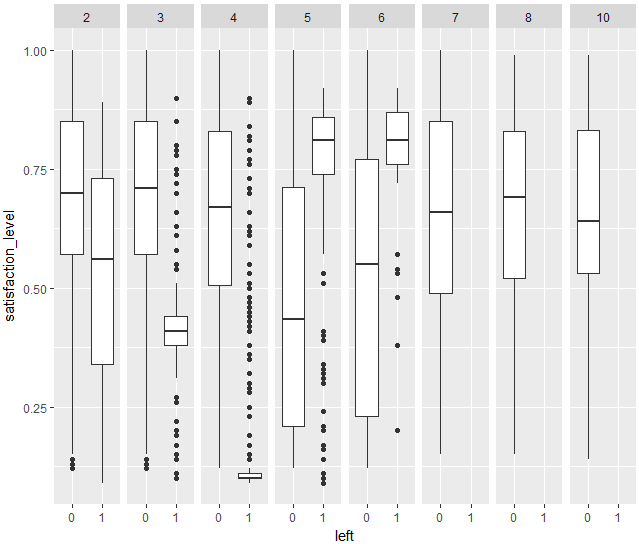これを見ると、たしかに、time_spend_companyが5または6である条件と、満足度が高いという条件が合わさると相乗作用によって、やめやすくなる(left=1)という仮説が立ちます。一応ヒストグラムの方も見ておきましょう。
ggplot(data=d, aes(x=satisfaction_level, fill=left))+
geom_bar()+
facet_wrap(~ time_spend_company, nrow = 2)
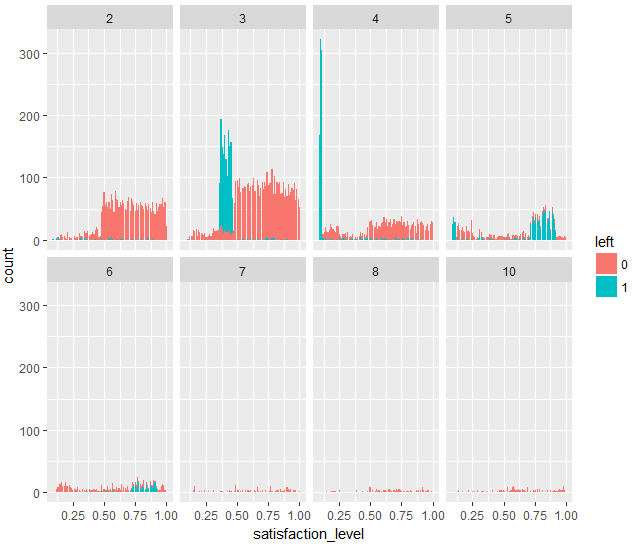交互作用項の検出という意味では、time_spend_companyが5または6が検出できれば十分なんですが、どのような人が辞めるかということを考えると、satisfaction_levelが0.37-0.5でかつtime_spend_company=3の社員、satisfaction_levelが0.12以下でかつtime_spend_company=4の社員は、会社を辞める傾向が強そうです。アンケートでこのような社員を見つけたら、会社での滞在時間を減らすような根本的な解決策を実行するか、何らかの方法で、仕事への満足度を上げる必要がありそうですね。

では次に行きたいと思います。
(1-5)last_evaluation:number_project3
(1-6)last_evaluation:number_project6

まずは、箱ひげ図から見てみましょう。
ggplot(data = d, mapping = aes(x = left, y = last_evaluation)) +
geom_boxplot()+
facet_wrap(~ number_project, nrow = 1)
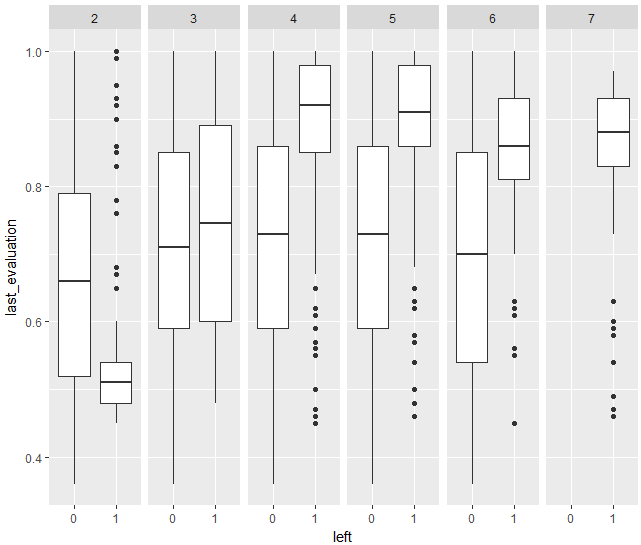last_evaluationとnumber_projectの交互作用項の候補としては、number_project=4,5,6,7がありえそうです。しかし検出されているのは、number_project=3,6です。

ヒストグラムもプロットしてみましょう。
ggplot(data=d, aes(x=last_evaluation, fill=left))+
geom_bar()+
facet_wrap(~ number_project, nrow = 1)
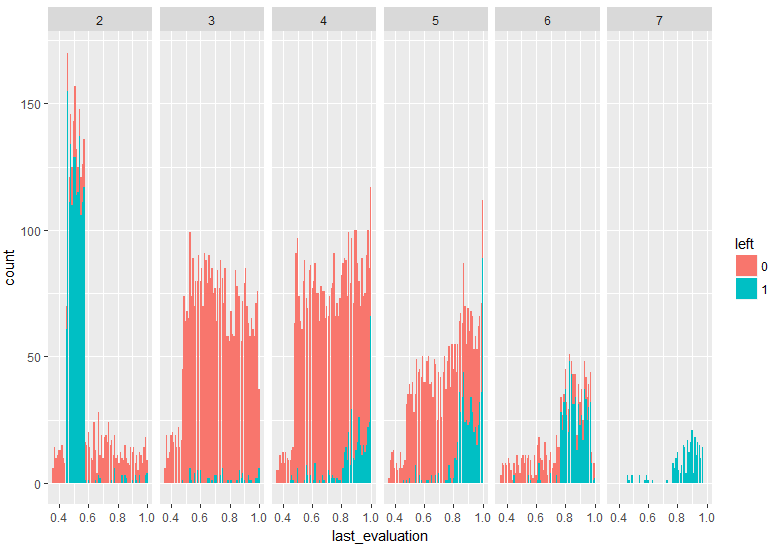これで、number_project=3,6が検出された理由がなんとなくわかりましたね。
last_evaluationとnumber_project=3の組み合わせが検出されたのは、last_evaluationが高いこととnumber_project=3という条件では、社員が辞めにくいことに対して相乗効果が考えられるためです。

last_evaluationとnumber_project=6の組み合わせが検出されたのは、last_evaluationが高いこととnumber_project=6という条件では、社員が辞めやめることに関して相乗効果が考えられます。

ヒストグラムの全体を俯瞰してみると、プロジェクト数が2でlast_evaluationが0.45-0.60の低評価の人はほぼ間違いなくやめるということ。プロジェクト数が4,5,6となってくると、辞める人ほど、辞める前の評価が高いことがわかります。
優秀な人を辞めさせないようにする解決策として、評価が高く、持っているプロジェクト数が4個以上の社員には、プロジェクト数を3か4個に減らすことが考えられますね。

では次に参りましょう。
(1-7)last_evaluation:time_spend_company3
それでは、箱ひげ図をプロットしてみましょう。
ggplot(data = d, mapping = aes(x = left, y = last_evaluation)) +
geom_boxplot()+
facet_wrap(~ time_spend_company, nrow = 1)
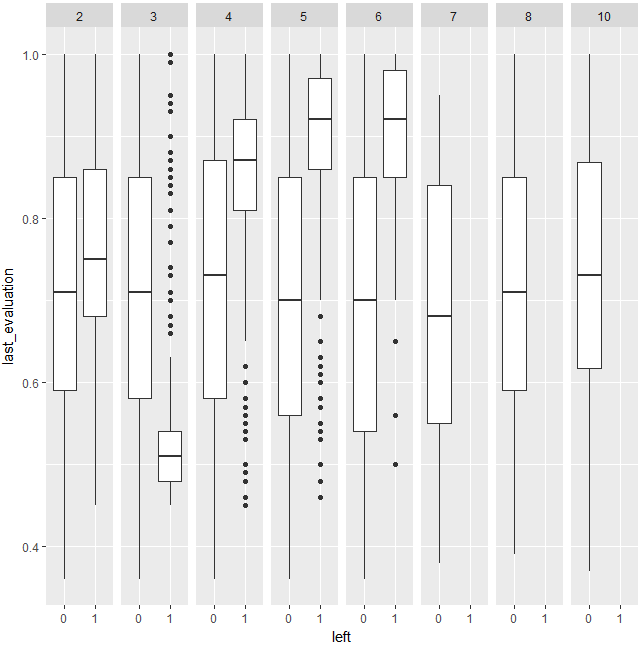time_spend_company=4,5,6あたりがが検出されていてもよさそうですが、実際に検出されているのは、time_spend_company=3です。これは、time_spend_company=3という条件と、last_evaluationが高いことが組み合わさると、辞めにくいとう相乗効果があると解釈できるでしょう。
一応、ヒストグラムもプロットしておきます。
ggplot(data=d, aes(x=last_evaluation, fill=left))+
geom_bar()+
facet_wrap(~ time_spend_company, nrow = 2)
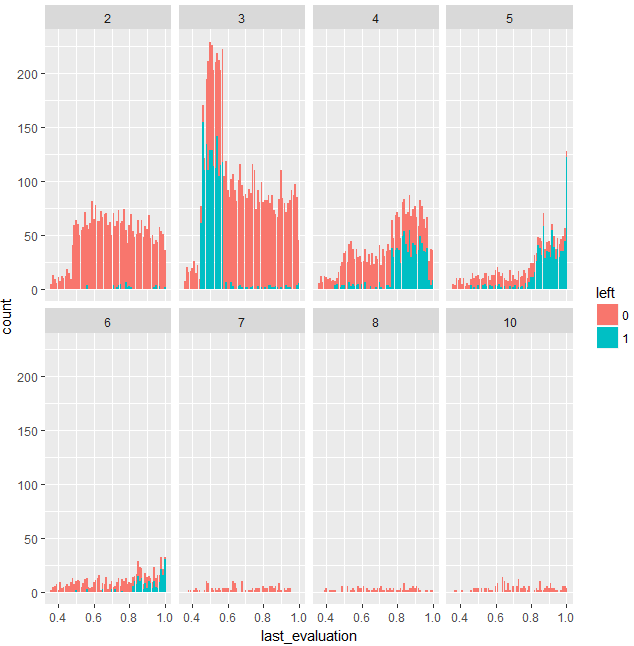これを見ると、time_spend_company=4,5,6も検出しておいてほしかったなと思いますが、相乗効果というには小さい変動なのでしょう。ただ、0.8以上の評価でかつ time_spend_company=4,5,6であれば、社員が辞める確率は高くなるとは言ってよいと思います。今回はtime_spend_company=3が検出されたのですが、この合計勤務時間で辞める人は、評価の低い人たちなので、優秀な社員を会社にとどめておくという立場からすると、time_spend_company=4,5,6のカテゴリの方が重要ですね。優秀は人を辞めさせない対策としては、time_spend_company=4,5,6のカテゴリでかつ評価の高い人には、会社への滞在時間を減らすような対策をとったり、辞めたいと思う理由を突き止めて、適切な対応をすることが重要と言えます。

(1-8)number_project3:average_montly_hours
それでは、箱ひげ図をプロットしてみましょう。
ggplot(data = d, mapping = aes(x = left, y = average_montly_hours)) +
geom_boxplot()+
facet_wrap(~ number_project, nrow = 1)

ヒストグラムもプロットしておきましょう。
ggplot(data=d, aes(x=average_montly_hours, fill=left))+
geom_bar()+
facet_wrap(~ number_project, nrow = 1)
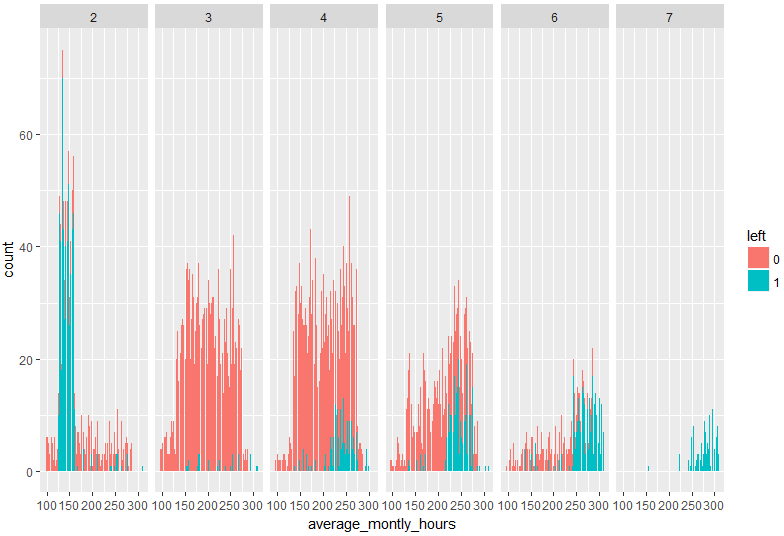average_monthly_hoursとの交互作用を検出しているのは、number_project=3ですが、number_project=3のときは、ほとんどの人が辞めないので、今回のsolutionには活かせなそうです。number_project=4,5,6,7では、月の平均勤務時間が増えるほど辞める人が増えるので、基本的に、月の平均勤務時間はnumber_project=4以下だと良さそうですね。

それでは次に行きたいと思います。
(1-9)average_montly_hours:time_spend_company5
まず箱ひげ図をプロットします。
ggplot(data = d, mapping = aes(x = left, y = average_montly_hours)) +
geom_boxplot()+
facet_wrap(~ time_spend_company, nrow = 1)
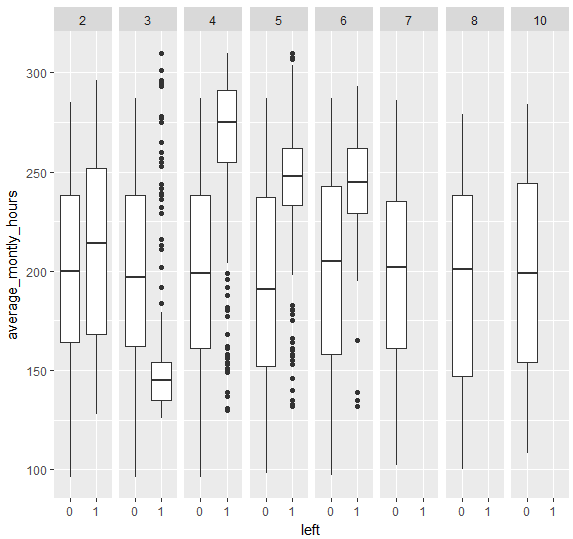箱ひげ図の結果だと、time_spend_company=4,5,6の時に、average_montly_hoursが高いほどleftが1になりそうとみてとれますね。

ヒストグラムもプロットしておきましょう。
ggplot(data=d, aes(x=average_montly_hours, fill=left))+
geom_bar()+
facet_wrap(~ time_spend_company, nrow = 2)

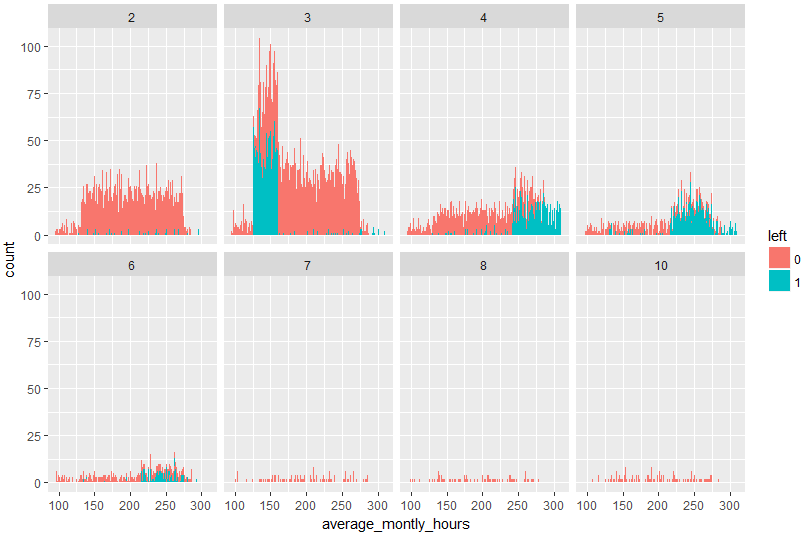
ヒストグラムの結果を見ても同様です。time_spend_company=4,5,6の時に、average_montly_hoursが高いほどleftが1になる傾向があることがわかります。
このヒストグラムを俯瞰すると、合計労働時間(time_spend_company)=3の時に、月平均労働時間(average_montly_hours)が125-175の社員が大量にやめ、合計労働時間(time_spend_company)=4,5,6の社員のうち月平均労働時間(average_montly_hours)が225以上の社員が辞め安いことがわかります。このようにして辞める可能性の高い人は特定できることがわかります。
辞める原因が労働時間にあるのかわかりませんが、アンケートをろおるなり聞き取り調査するなりすれば原因はわかるでしょう。

今回は、かなり長くなってしまったのでここでいったん終わりにします。
今回終わらなかった、(2-1)-(3-2)は次回やっていきたいと思います。

鈴木瑞人
東京大学大学院　新領域創成科学研究科　メディカル情報生命専攻　博士課程
東京大学機械学習勉強会　代表
NPO法人Bizjapan Technology部門 BizXチームリーダー