賢いサルならわかるかもしれない正規分布

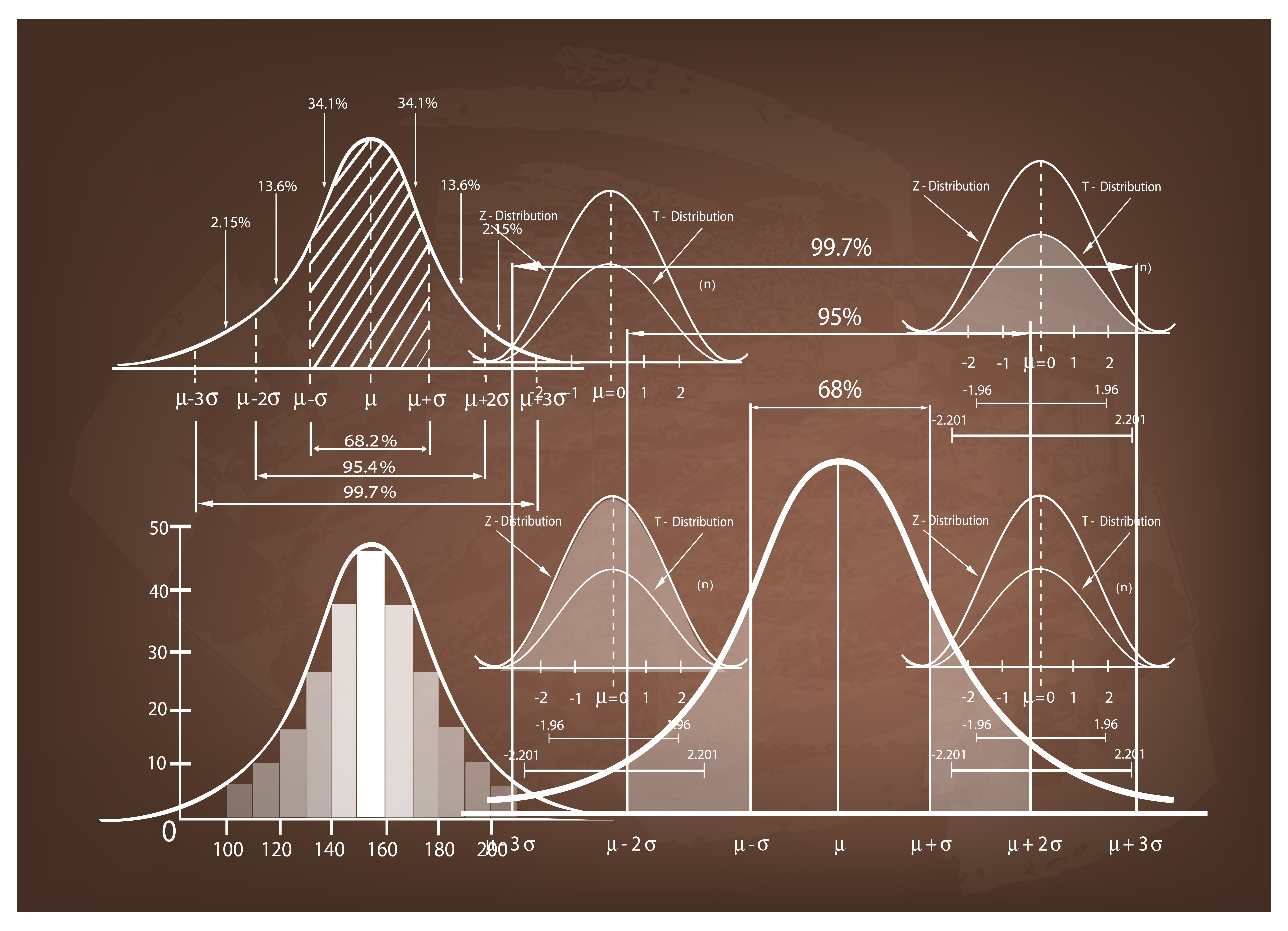みなさんは、正規分布という言葉を聞いたことがありますか？
最近では、高校の数Bにて、学習指導要領の範囲内で扱われており、文系理系問わず知られているようです。
僕が高校生の時は、数Bと言ったら、ベクトルと数列でしたが、今や、”確率分布と統計的な推測”が数Bのメインの一つとして入っているとのことです。
データサイエンスの時代に合わせた配慮なのでしょうね。

それでは、今回は、正規分布について説明していきます。
まずは、正規分布がどんな分布化を見るために、R言語にて、正規分布に従う乱数を発生させて、そのヒストグラムを作成していきましょう。
#平均0,標準偏差1の正規分布に従う乱数を1000個生成
d=rnorm(1000,0,1)
#データの構造を見てみる
str(d)
#ヒストグラムの作成
hist(d)
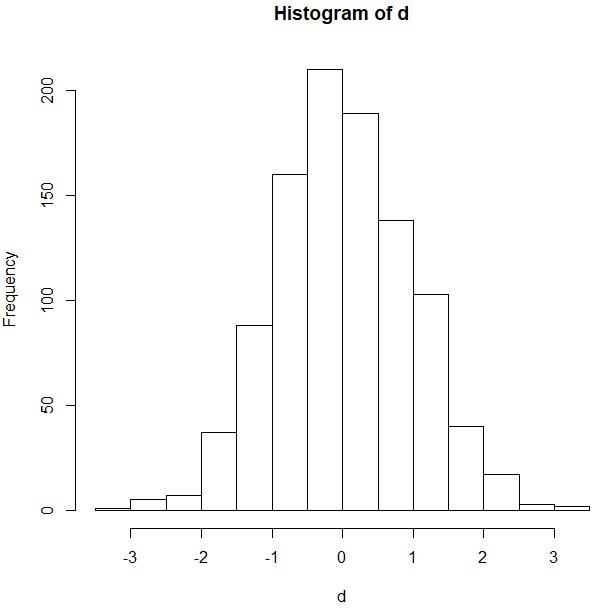このヒストグラムの見方ですが、まず縦軸は、データの個数を表しています。そして横軸は、データの値の範囲を表していまして、左から、-3より小さいデータが1つ、-3以上の-2.5より小さいデータが6つ、-2.5以上-2より小さいデータが13つ、というようになっています。
正規分布は、左右対称の分布であり、今回も、0を中心にしてほぼ左右対称の分布となっています。

正規分布の活用方法はいくつもあり、個人的には、重回帰を行う際の誤差項としての価値が最も重要だと思っているのですが(商品の売り上げ予想とか、イベントの来場者人数の予想、店舗への来店人数の予測などに使う)、これについては、すでにいろいろな人に話しているので、今回は違った観点から、正規分布を見ていきます。

先ほどは、Rにおいてデフォルトで使える関数であるrnorm関数を使用して、正規分布に従う乱数を生成しました。

しかし、rnorm関数を使ってしまうとブラックボックスでよくわからないですね。

アプローチを変えましょう。

そもそも正規分布とはどんなものでしょうか？

それを知るには、正規分布の定義式である、”正規分布の確率密度関数”を知る必要があります。
すべての分布には、それに対応する”確率密度関数”が存在します。

~~正規分布の確率密度関数~~

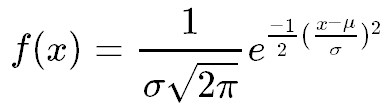
という式になります。
一見すると複雑な式に見えますね。

σ(シグマ)とμ(ミュー)がパラメータで、π(パイ)は3.14…というご存じ円周率で、e(エクスポネンシャル)は、2.717..というネイピア数です。
まず描画してみましょう。μ=0,σ=1で描画します。
#関数f(x)を作る
FUN = function(x){(1/(1*sqrt(2*pi)))*exp(-(1/2)*((x/1)^2))}
#描画
plot(FUN,-4,4,ylab=”probability”)
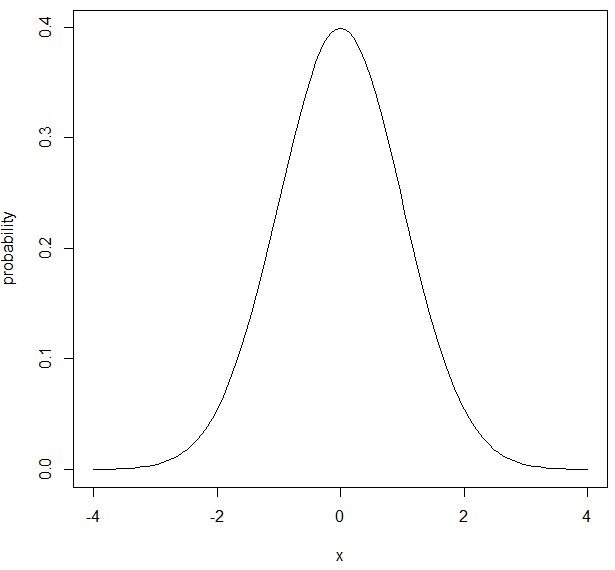これの見方なんですが、縦軸は正規分布に従う乱数(普通の実数)が、発生する確率を表しています。

つまり、0周辺の数が発生する確率が著しく高く、3以上または-3以下の数が発生する確率はほぼ0ということです。
この描画の結果から、平均μ=0、標準偏差(データのばらつきの度合い)σ=1である正規分布に従う乱数(普通の実数だと思ってください)は、0周辺の数が最も多く、次に1と-1周辺の数が多く、次に2と-2周辺の数が多く、3以上または-3以下の数はめったに生成しないことがわかります。

さて、正規分布の確率密度関数については、少しご理解いただけたかと思います。どういう数が、それぞれどのくらいの確率で、生成するかを示した関数なんですね。

では次に、シンプルさが好まれる”数式”が、なぜ、こんな”ごっつい”式になってしまったのかをご説明します。

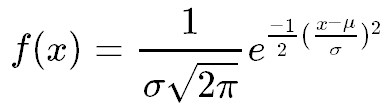
実はもともとはかなりシンプルな式でした。
こんな感じです。シンプルですね。
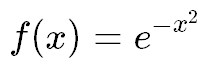なぜ、シンプルな形が採用されず、上の複雑な式が採用されたかをご説明しましょう。
みなさんは、ボタンがなくて操作できないスマホと、ボタンが2つあって操作できるスマホ、どちらがほしいですか？(スマホでもPCでも何でもいいですが)ボタンが2つあったほうがいろんな状況に対応できて良さそうですね。
ここでの”ボタン”は、パラメータμとσを指します。
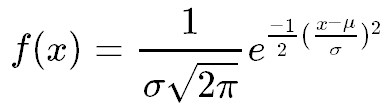この式でまずボタンμを-1,0,1といじってみましょう(σは1で固定)
FUN = function(x){(1/(1*sqrt(2*pi)))*exp(-(1/2)*(((x+1)/1)^2))}
FUN2 = function(x){(1/(1*sqrt(2*pi)))*exp(-(1/2)*(((x-0)/1)^2))}
FUN3 = function(x){(1/(1*sqrt(2*pi)))*exp(-(1/2)*(((x-1)/1)^2))}
plot(FUN,-4,4,col=2,ylab=””)
plot(FUN2,-4,4,col=1,add=T)
plot(FUN3,-4,4,col=3,add=T)
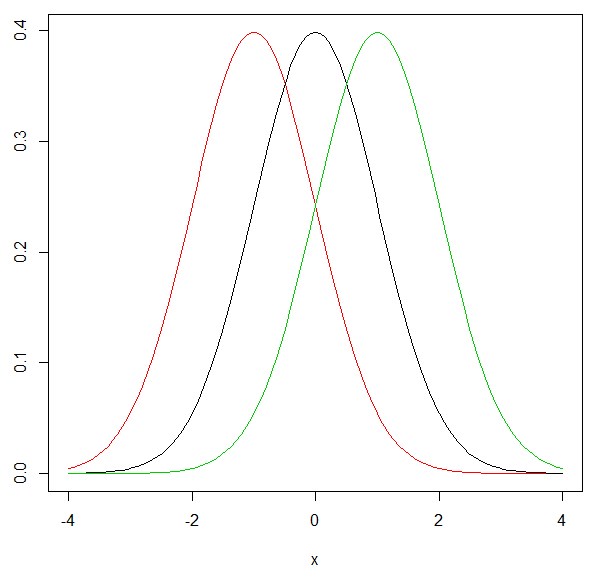赤(左)がμ=1,黒がμ=0,緑(右)がμ=-1です。確かにμは正規分布の確率密度関数の結果を、グラフの(x軸に平行な)平行移動という形で、柔軟に変えてくれるようです。

次に、σというボタンを、0.5,1,2といじってみましょう。
FUN = function(x){(1/(1*sqrt(2*pi)))*exp(-(1/2)*((x/1)^2))}
FUN2 = function(x){(1/(2*sqrt(2*pi)))*exp(-(1/2)*((x/2)^2))}
FUN3 = function(x){(1/(0.5*sqrt(2*pi)))*exp(-(1/2)*((x/0.5)^2))}
plot(FUN3,-4,4,col=3,ylab=””)
plot(FUN2,-4,4,col=2,add=T)
plot(FUN,-4,4,col=1,add=T)
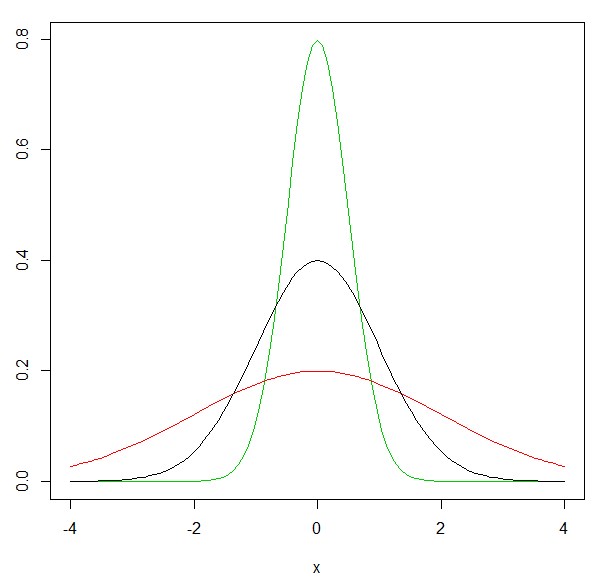σ=2が赤、σ=1が黒、σ=0.5が緑です。
確かにσというボタンが、正規分布の確率密度関数の結果を変化させているのがわかります。
シンプルだけど操作できないスマホ

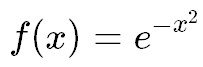
より、一見複雑そうだけどもボタン(μとσ)が二つあって操作できるスマホ
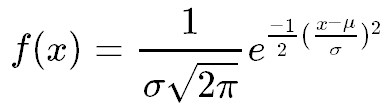の方がよいことはご理解いただけたかと思います。

それでは次に少し違った視点(ボタンの内ないスマホからボタンのあるスマホができた流れ)をご紹介していきます。

まずこの関数
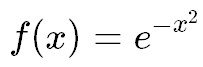 を描画してみましょう！
#関数の作成
FUN = function(x){ exp(-(x)^2) }
#描画
plot(FUN,-4,4)
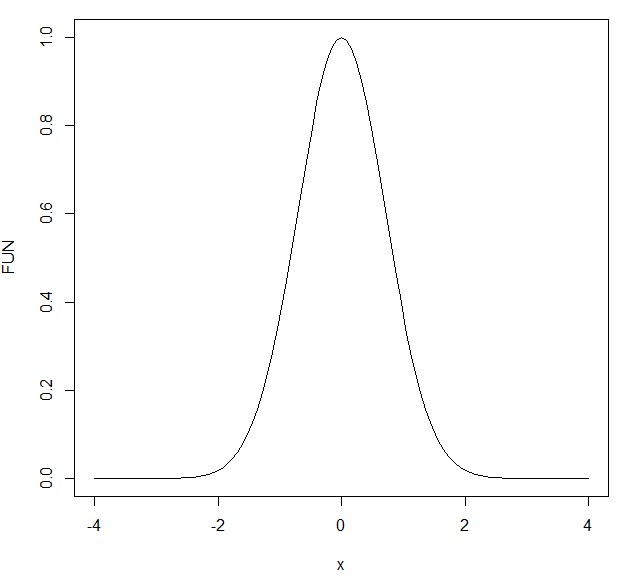これは、ｘ＝0に関して左右対称で、まさに正規分布の形をしています！
しかし問題が一つあります。”確率密度関数”は、”確率”なのでこの曲線の下の面積は、合計1である必要があるんですね。
どういう事かというと、正規分布に従う乱数を生成すれば、このx軸上の数のどれかが必ず生成するわけです。なので、確率を足し合わせると、その和が”1″になる必要があるんです。その和というのは、ここでいうと、確率密度関数による曲線と直線y=0の間の面積になります。以下でこの部分に色付けして見やすくしていきます。

曲線の面積は以下のグレーの部分で、計算すると、√π(ルートパイと読む)になります(ガウス積分の公式使います)。
#点群を生成
x = seq(-4, 4, length=1000)
y1=exp(-(x)^2)
y2=rep(0,1000)
#関数f(x)の下の部分と直線y=0で囲まれた部分を灰色で塗る(真ん中の上の斜めの線は気にしないでください)
segments( x,y1, x,y2, col=”gray”)

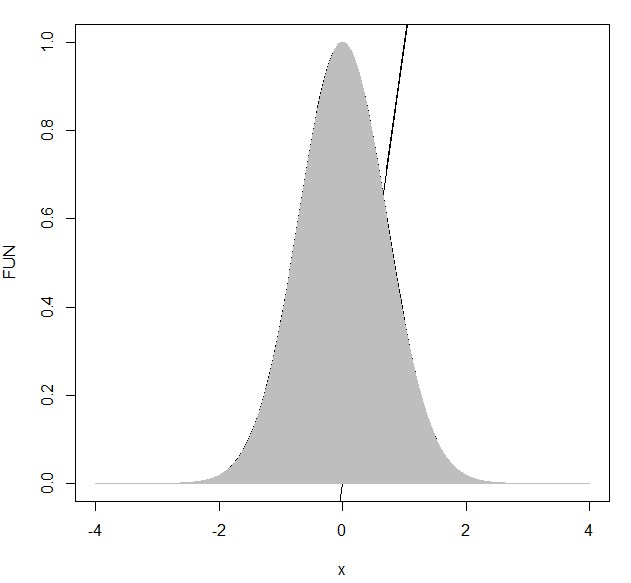
この灰色の部分の面積が√πということは、この面積を√πで割れば、1になり、晴れて確率密度関数となることができます。
これで、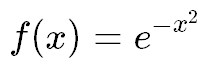は、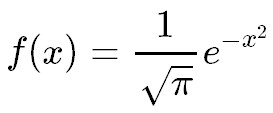という形に変形できました！

ここからが少し難しいのですが、正規分布の形状をいろいろ変えられると後で便利なことがいろいろあるため、xをσで割るという形式にします。シンプルに考えるため、μ=0として考え数式としては次のようになります。

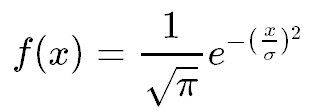
いろいろ描画していきましょう。
#σ=1の時(黒)
FUN = function(x){ exp(-(x/1)^2) }
plot(FUN,-4,4)
#σ=2の時(赤)
FUN2 = function(x){ exp(-(x/2)^2) }
plot(FUN2,-4,4,col=2,add=T)
#σ=0.5の時(緑)
FUN3 = function(x){ exp(-(x/0.5)^2) }
plot(FUN3,-4,4,col=3,add=T)
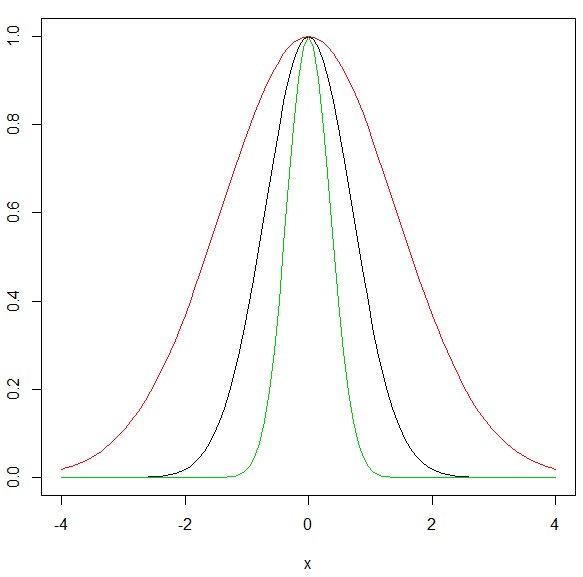黒(σ=1)は、普通の正規分布ですね。
赤(σ=2)は、横に広がった分布になっています。
緑(σ=0.5)は、正規分布より、キュッと中心に絞られた分布になっています。
このようにσを、1,2,0.5と変化させると形状変化するのはわかりました。
しかしこのままだと明らかに、各曲線とy=0の間の面積が、変化しています。

eの指数に1/2を掛け、eの係数に1/(σ√2)をかけて補正しているのですね。
数式で改めて書くと、

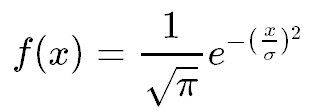を、
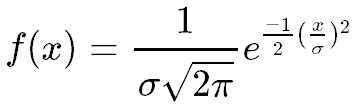と補正しているわけです。実際にこれを-∞～∞の区間で積分すると1になります。

さて最後に、今の3つの関数をそれぞれ補正して、曲線と直線y=0の間の面積が1になるような式にして、3つ重ねて描画してみようと思います。
FUN = function(x){(1/(1*sqrt(2*pi)))*exp(-(1/2)*((x/1)^2))}
FUN2 = function(x){(1/(2*sqrt(2*pi)))*exp(-(1/2)*((x/2)^2))}
FUN3 = function(x){(1/(0.5*sqrt(2*pi)))*exp(-(1/2)*((x/0.5)^2))}
plot(FUN3,-4,4,col=3,ylab=””)
plot(FUN2,-4,4,col=2,add=T)
plot(FUN,-4,4,col=1,add=T)
3つの曲線と直線y=0が囲む面積が等しくなったのがわかるかと思います。実際それぞれ1になっています。
黒がσ=1、赤がσ=2(潰れた形状)、緑がσ=0.5(とがった形状)をしており、それぞれは、直線x=0に関して対象です。

さて、上の式をもう一度書くと、
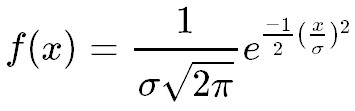です。これをx軸方向にμ平行移動し、x=μを中心とした正規分布になるようにすると、確率密度関数は、
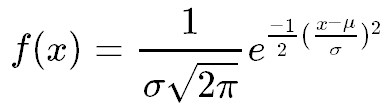となり、正規分布の、確率密度関数にたどり着きました！
(ガウス積分の公式を使って、-∞～∞の区間で積分(y=x-μとする置換積分)するとf(x)はちゃんと1になります)
難しいようで、意外と簡単でシンプルだったんですね。正規分布の確率密度関数は。

今日は、この式のありがたさを実感するまではいけないのですが、将来的に、例えば重回帰分析や状態空間モデルなどに到達すれば、ありがたさを実感するにいたるでしょう。

では、今回はここまで。

鈴木瑞人
東京大学大学院新領域創成科学研究科　メディカル情報生命専攻　博士課程
東京大学機械学習勉強会　代表
NPO法人 Bizjapan Technology部門 BizXチームリーダ